This is a useful GUI module. It saves using conversion from GUI to DSP and back to GUI if you need to use math functions on a GUI float value. It works like the DSP Float Function module, with one notable difference, like most GUI modules it works in both directions. So as well as the A conversion formula, you need to specify the B conversion formula which is the inverse of the A formula;
so if the B formula was A*100, then the A formula must be B/100.
Note:
The A formula is applied to the value received by Plug B and is output from plug A The B formula is applied to the value received by Plug A and is output from plug B.
Note: If you only need the conversion to work in one direction, then there is no need to bother with the inverse formula.
Note: If either the A or B function is left as an empty string or the value 0, signal flow from that pin will be disabled.
Inverse functions; links to more information.
For those who don’t understand Inverse Functions and how to find the inverse of a function, there is detailed information and explanantions of Inverse Functions on these websites;
About inverse functions
Another article on inverse functions
Online inverse fuction calculator (Wolfram Alpha)
Supported Math functions:
All the frequently used math functions are supported; multiply, divide, add, subtract, power, sin, cos, tan, asin, acos, atan, sinh, cosh, tanh, exp, log, log10, sqrt, floor, ceil, abs, hypot, deg, rad, sgn, min, max.
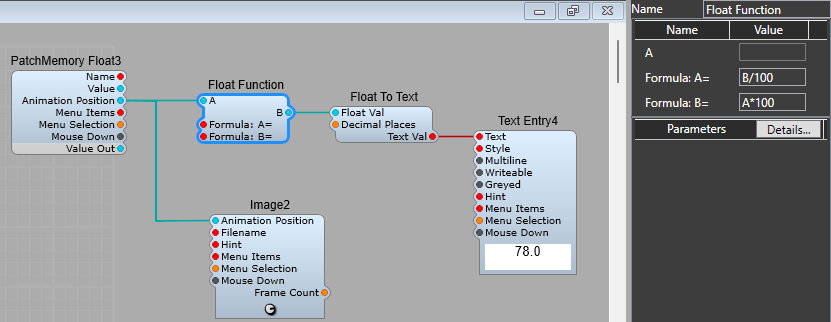
Example Float function usage.
Suppose you want to have a knob control’s readout display the slider value from 0 to 100, but you want to keep the actual control value in the default 0 to 10 range.
This allows you to alter the displayed value, and by using the inverse function we are also allowing the user to enter a value (between 0 and 100) in the text box to change the control knob’s position and output, but still keep the control value inside it’s default range.
The formula and it’s inverse can either be entered into the modules properties panel, or supplied as a text string to the appropriate plugs.
How the VU Meter uses Float Function.
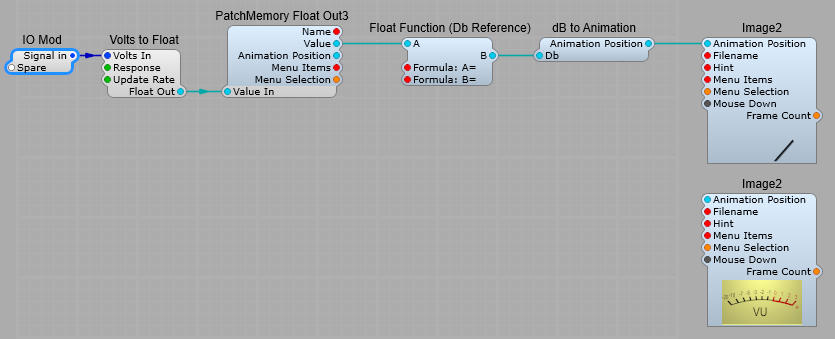
Another use for the GUI Float Function is demonstrated in the VU Meter.
We take the Audio input, and feed it into the Volts to Float module where the signal level is converted to floating point at a rate optimised for DSP, which will also give a suitable response time for the meter to be useful (Conversion rate = 60Hz), and the type of response is set to dB VU to suit a VU meter readout.
The next step is to use a PatchMemory Float Out3 to convert the data from Audio/DSP to GUI, and to take the value output (not the Animation Position output) and feed it via the Float Function with these values for the Formulae:
Formula A= B-18
Formula B= A+18
From here the data is sent via the dB to Animation module to convert the data to fit the scale used for the VU meter, this is where we finally use Animation Position to move the “meter” to the position that matches the Audio input on the VU “scale”.
The actual meter we see on the panel uses two Image2 modules. The top one which displays the meter needle is connected to the Animation Position data, and the lower Image has no connections as it’s just the meter scale.
Attack, Decay, and Release time display using Float Function.
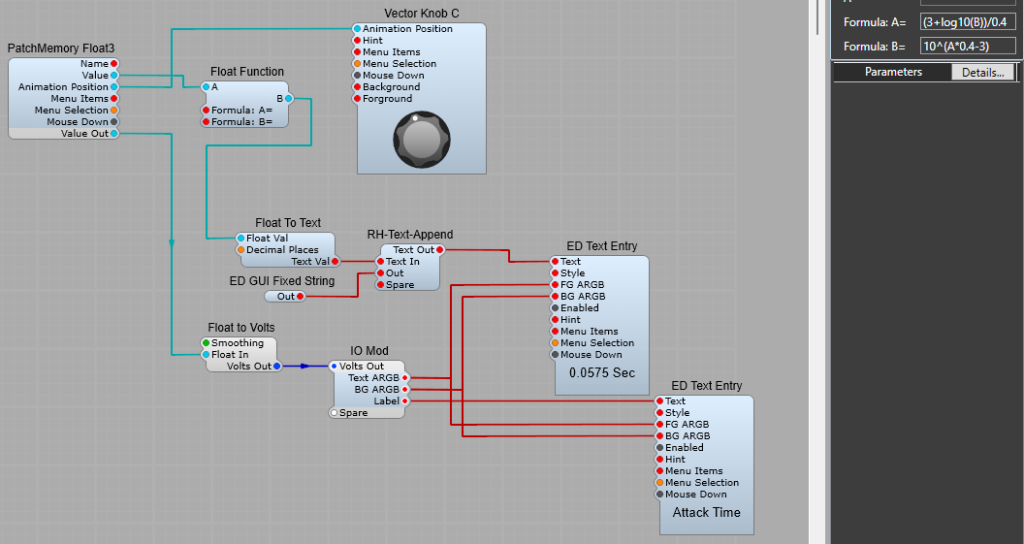
We can also use the Float Function to display the Attack, Decay, or Release time of the ADSR modules. The layout below does the job quite neatly. (You could use all stock modules but then you won’t have the text append function, or control over how the Value and Label Text Entry look on the Panel).
Applying the math formulae for the conversion.
The formula to convert the Volts (or in our case, GUI float, as it’s not yet DSP Volts) to ADSR timing is 10^(A*0.4-3)
Because we want to convert the Float Value to ADSR timings the converted value needs to appear on the B Plug, so this is formula B.
To convert a text entry to the Float Value for the ADSR timing we need to the inverse of this formula as Formula A which is (3+log10(B))/0.4
Both the Formulae.
Formula A is (3+log10(B))/0.4
Formula B is 10^(A*0.4-3)
If you study these two formulae carefully you can see just what is meant by an Inverse Formula, we are just working out how to perform the exact reverse of the original math function. (Add becomes subtract, multiply becomes divide and so on. It may seem at first look a bit random, but there is a logical structure in finding the inverse of a math formula…)
Having both the A and B formulas allows you to control these times from either the knob or the text entry box.
Leave a Reply