Applying the basics of Formant Synthesis.
The basic idea is to take three bandpass filters connected in parallel. Here we use three SV filters set to their 2 Stage Bandpass mode, each one followed by a Level Adj module so we can adjust the three parameters we need:
1) Frequency
2) Resonance or “Q”
3) The audio level of each filter.
Each of these three filters represents a Formant.
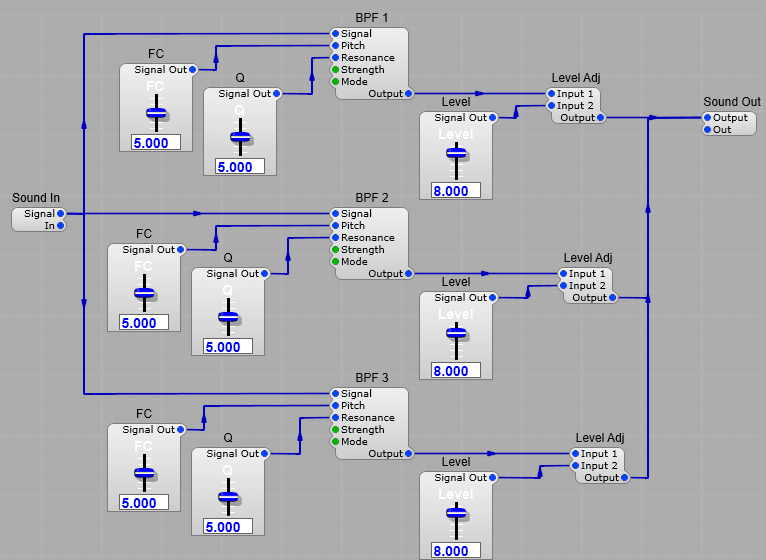
By connecting white noise to the input and a frequency analyser to the output we can see the filter in operation- (by using white noise it’s easier to see the resonant peaks than it is with a pulse or sawtooth). You can see below how I have set some frequencies and the resonant peaks corresponding to those frequencies are clearly visible.
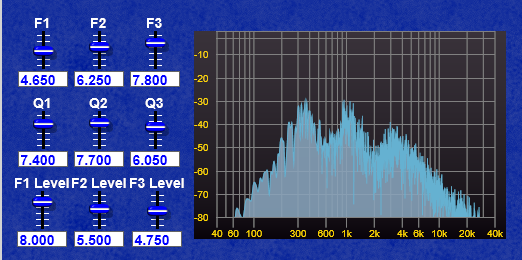
This method has some disadvantages though;
1) The stock SV filters are fixed into 1 Volt per Octave for the Pitch control meaning we have to do some maths and use extra modules to convert the readout into a Hz or kHz readout.
2) The stock SV filters tend to oscillate and ring at high resonance levels.
3) Three separate filters, and the maths and extra modules for displaying the filter frequency will all add to the CPU use.
A more Efficient Formant filter.
Fortunately there is a purpose built filter module in the TD modules range, the TD_SVX4.
It is a module that does the job of four SV filters, with the advantage that the Frequency control voltage is 1 Volt per kHz, making readout easier, and they are optimised so as not to “ring” or oscillate at high resonance levels.
This makes quite a neat and more CPU efficient solution for a Formant filter.
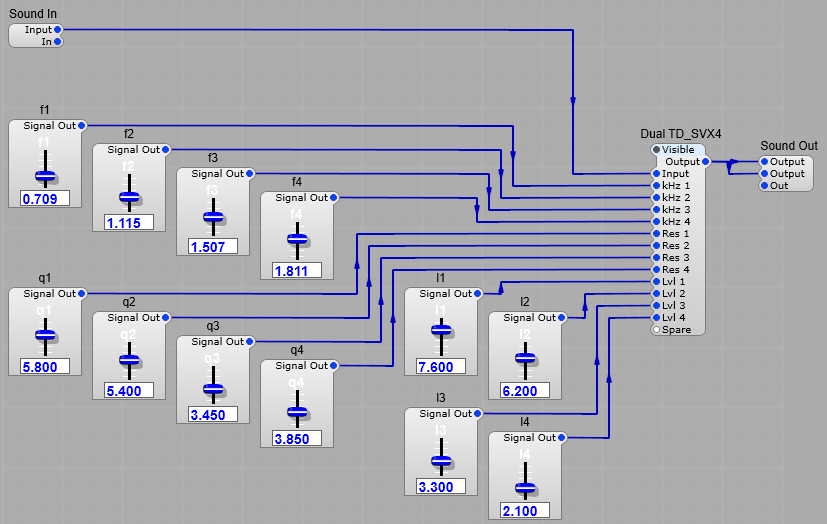
The structure of the dual TD_SVX_4 container is shown below. I used two filters to get a steeper bandpass response. You can see below the filter in operation with the four resonant peaks (again using a noise input). Even at maximum resonance there is no ringing or oscillation
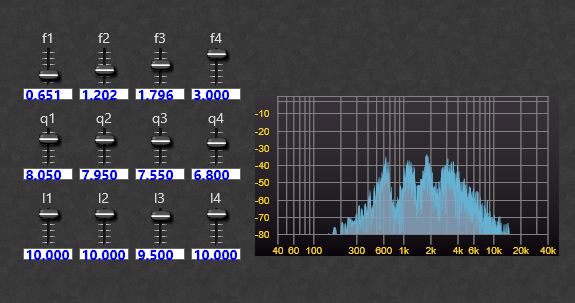
Not just for speech.
By their nature acoustic instruments also have resonant frequencies, so we can use our formant filter to make more accurate imitations of acoustic instruments by adding resonances to their audio spectrum. The chart is shown below, note how some resonances are quite broad compared to others.
| Instrument | F1 | F2 |
| Flute | 800 | … |
| Oboe | 1400 | 3000 |
| English Horn | 930 | 2300 |
| Clarinet | 1500-1700 | 3700-4300 |
| Bassoon | 440-500 | 1220-1280 |
| Trumpet | 1200- 1400 | 2500 |
| Trombone | 600-800 | … |
| Tuba | 200-400 | … |
| French Horn | 400-500 | … |
| Cello | 300 | 500 + 900 |
| Double bass | 70 | 250 |
| Viola | 220 | 350 |
| Violin | 503 | 1600 |
| Acoustic guitar | 90-150 |
More on acoustic instruments and formants.
Note: The Formant frequencies of acoustic stringed instruments are by no means set in stone. These vary from instrument to instrument, as there are a large number of variables affecting the sound, such as differences in construction, differences in materials etc. Different styles and models of acoustic guitar will have different resonances, but generally speaking the resonance will be in the lower frequency end of the scale as these are the weaker frequencies and need boosting to make the sound project evenly across the playing range.
Even “classical” instruments such as Violin and Viola will have different resonances due to the way they are constructed.
The best way to find the frequencies for these instruments is experiment, and find the sound that seems right to your ears, and experience of acoustic instruments.
Leave a Reply