Synthedit help and tutorials

Stuck with a SynthEdit project?

Month: February 2025 (Page 2 of 2)

Basic “Analogue” Subtractive synthesis.

21/02/2025 / / 0 Comments

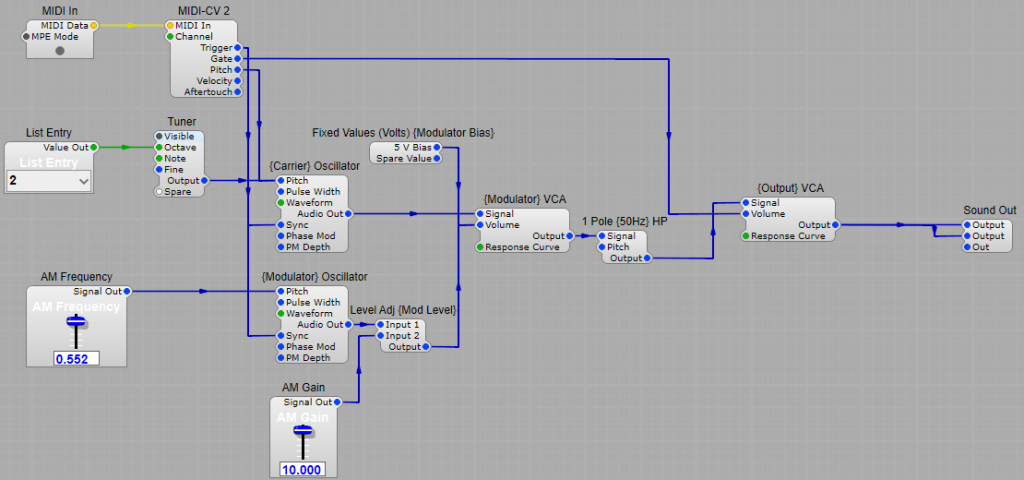
The concept of the Synthesizer.

Subtractive synthesis is one of the oldest approaches to synthesizing sounds electronically. Some say it started with the Moog… but there are synthesizers of a sort that pre-date the Moog. Even the Hammond organ and the Theremin are a form of synthesizer.

The building blocks of a synthesizer.

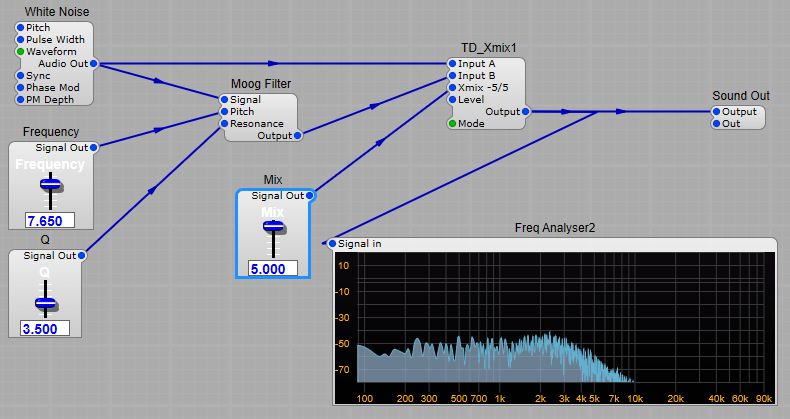
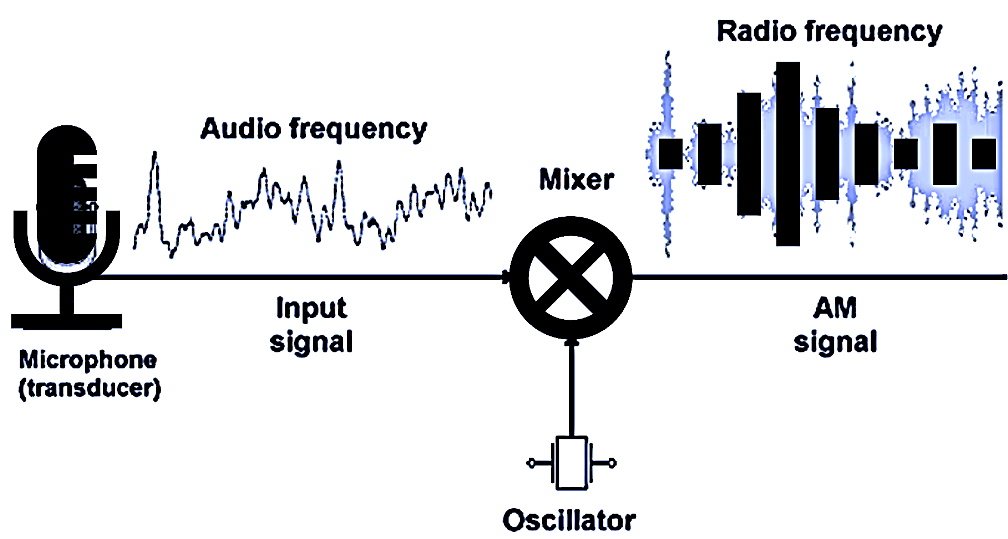
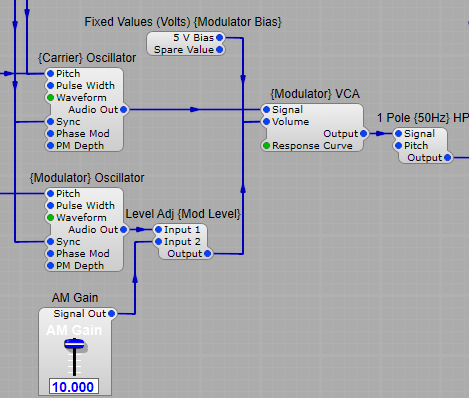
We start off with one or more voltage controlled oscillators (VCO) with a harmonically rich sound. Harmonics being the odd or even multiples of the oscillator’s frequency. Two or three oscillators can be mixed together in the mixer along with white or pink noise if required (a hissing sound).
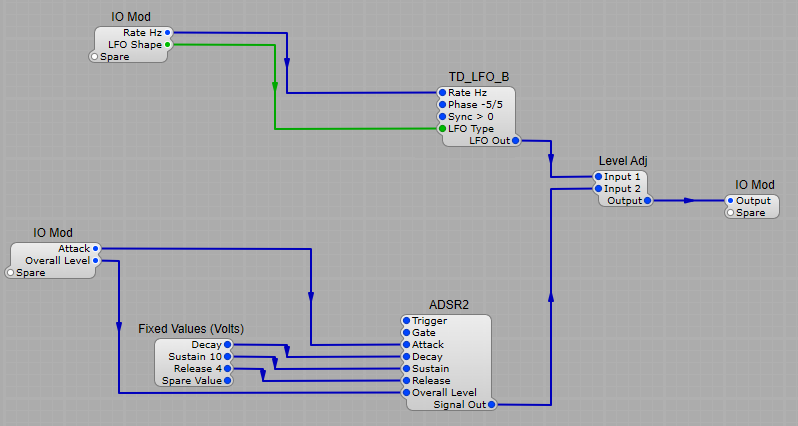
The LFO is just a lower frequency version of a VCO that can be controlled manually to produce tremolo, vibrato or filter sweep effects.
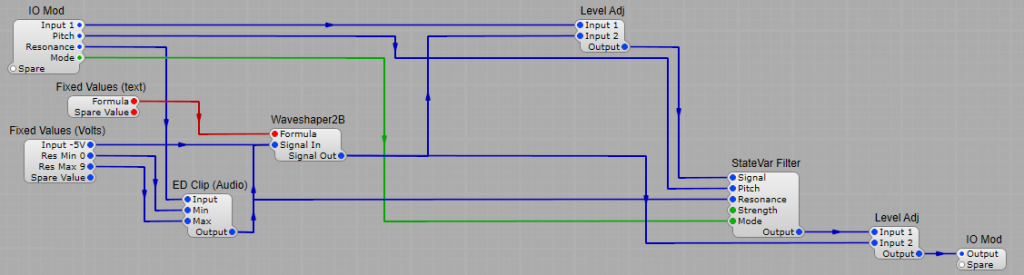
We then use a voltage controlled filter (VCF) using the resulting audio to boost and or cut certain frequencies. Various other methods of adding harmonics can be used before filtering such as wave-shapers, clippers and ring modulators (more about these later). The filters cut-off frequency can be modulated to provide some harmonic variation, followed by a voltage controlled amplifier modulated by an envelope wave form (ADSR) triggered by the keyboard. ADSR can also be used to modulate the VCF.
Using voltage control of pitch, timbre and amplitude gives so us a huge amount of flexibility and musicality in the instrument.
I’ll explain some of the key phrases here:

Voltage Controlled Oscillator (VCO)
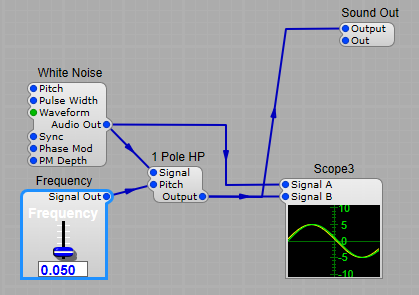
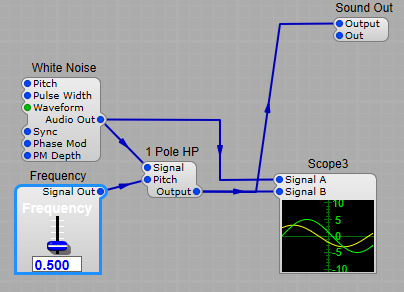
This produces our sound, the pitch of which is controlled by a voltage from the keyboard. It can be a simple pure sine wave with no harmonics, or a very rich sawtooth signal. Some of the types of waveform are shown below.

More about VCOs.


White/Pink Noise Generator, This produces a random audio signal producing a hissing noise useful for creating percussion, the sound of wind and rain, or “breath” effects for creating certain instruments.

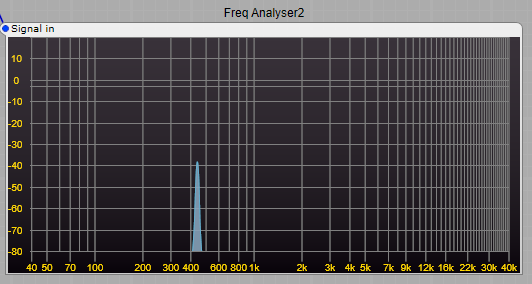
Voltage Controlled Filter (VCF), usually a low pass filter, this takes our sound from the VCO and filters it removing some of the higher frequencies from our audio. We can control the cut-off point for control over the timbre, and add some feedback to produce a more resonant sound. See the diagram below, that little peak at the cut-off frequency is where the resonance occurs. Filter cutoff frequency can be modulated using ADSRs’, LFOs’ and other control voltage generators.

However we are by no means limited to low pass filters… there are high pass, band pass, and notch filters too… and we can combine these filter types too…

More about Filters

Controlling the volume with a VCA and an Envelope Generator.

Voltage Controlled Amplifier (VCA), this does just what it says on the tin and controls the loudness of the sound leaving our synthesizer.
It really is as simple as using a varying voltage co control the volume of the sound.
More about VCAs
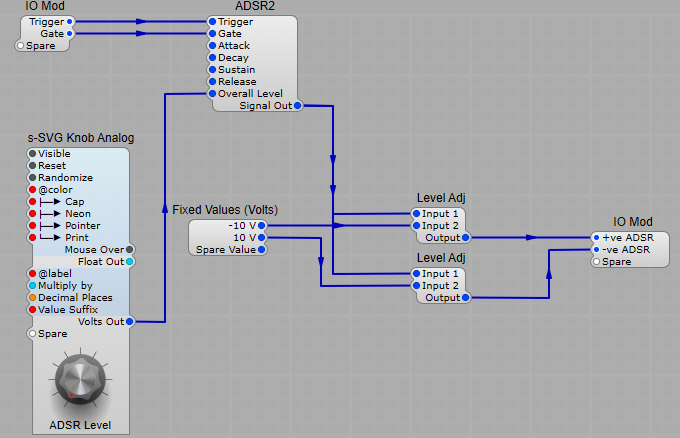
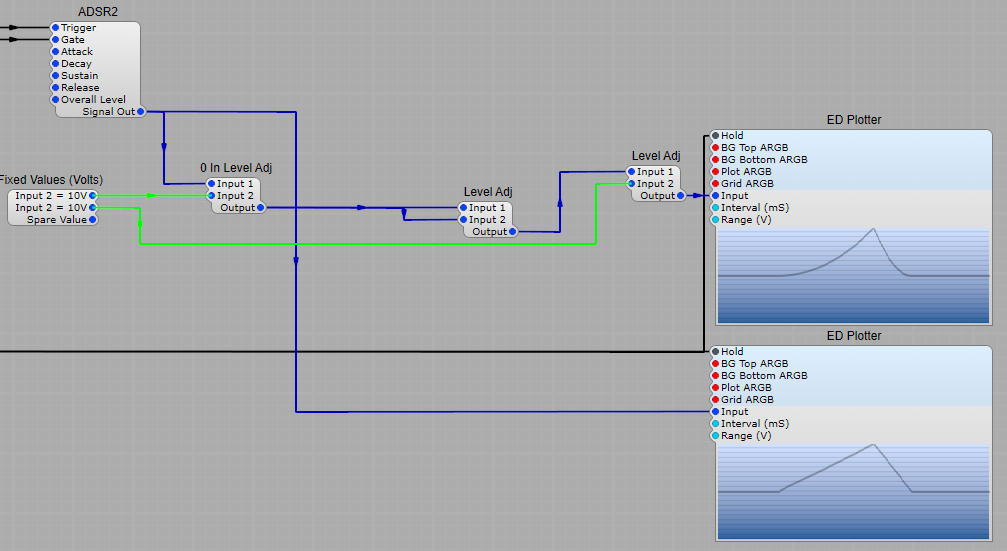
This is usually done with the Envelope Generator (EG also ADSR), OK so this might be a little confusing… why is the EG also ADSR? Well it generates a voltage which can be used to control both the VCF (sweep the cut-off frequency) and the VCA (the loudness of the audio).
Notice the shape of the envelope in the diagram below, it has four stages; 1) Attack (A), 2) Decay (D), 3) Sustain (S), Release (R).


The terms Envelope Generator and ADSR are often used interchangeably. However some early synthesizers just had Attack and Release controls, there was no decay control or control over sustain level.
More about ADSR

Getting More complex.

We are by no means limited to just these few modules. We can have as many oscillators as required, additional filtering, and other ways of altering the sounds we are generating.
Various other methods of adding harmonics can be used before filtering such as wave-shapers, clippers and ring modulators.

Related posts:

  1. Making a (very) basic Synthesizer in SynthEdit.

Level Adjust module.

15/02/2025 / / 0 Comments

The Level Adjuster multiplies the value received on the Input one plug by the value received on the Input two plug. It can be used for an effect similar to ring modulation (This is not true ring modulation, which is balanced and suppresses the carrier), or to apply an low frequency modulation to a signal (amplitude modulation), or to scale a control voltage or audio signal by a fixed/variable amount.
The two inputs are multiplied together, then normalized.
(e.g. 5V * 2 V = 1V, (5 * 2 ) / 10)
NOTE: To apply an volume envelope to audio from an ADSR module you should use the VCA module, as it changes the volume of the signal using a decibel scale, not the linear scaling of the Level Adjuster.
Using the Level Adj module in place of a VCA will result in an un-natural sounding envelope, the VCA module also uses less CPU.
The Level Adj module is intended for controlling the output of LFO’s and other control voltage modules, not for audio gain control. It can also be used for Tremolo and amplitude modulation of audio where you would expect to have a linear response to the gain voltage.

Note: When selecting the Level Adj module from the modules panel it has default values set of 8V on both the Input 1 and Input 2 plugs. It’s a good move to set these to 0 volts when adding the module, as you can get some unexpected offset voltages when these plugs are connected to an IO module and shared with another container.


Plugs.
Left Hand Side:
Input 1:- (Voltage) First input signal A
Input 2:- (Voltage) Second input signal B
Note if a negative voltage is applied to Input 2 the Level Adj will function as a variable gain inverter.
Right Hand Side:
Output:- (Voltage) Normalized Output signal = (A × B) ÷ 10
Note: Normalization of the output means that if the voltages on Input 1 (A)= 5V and Input 2 (B) = 2V then 5*2 = 25 the output voltage will be 25 ÷ 10 = 2.5 not 25V
and likewise if A= 6V and B = 3V then 6*3 = 18 once again the output voltage will be 18 ÷ 10 = 1.8

Using a Level Adj module as an inverter.

Using the Level Adj module in this way we can provide both +ve and -ve ADSR envelopes, and still have the overall level controlled in the usual way.

A delayed LFO using ADSR and a Level Adj module.

A delayed LFO is one that instead of being on permanently gradually fades in as a note is played. The Level Adj is ideal here as we would want a linear gain control for the LFO output. The ADSR is just wired up to provide a variable attack for the “fade in”, the overall level is used to provide the maximum level, Sustain is set at 10, and a fixed release of 4 is set so that the LFO output fades away rather than stopping abruptly after the key is released.

Converting Linear voltage “curves” to Exponential voltage curves.

By feeding the same input voltage to both input 1 and Input 2 of the Level adjuster we are effectively creating an exponential output. The first Level Adj module has Input 2 set to 10 volts so that the structure retains the original 0 to 10 V input scaling. You can see the effect of the module on the output of an ADSR 2 using an ED Plotter module (the bottom display is the Linear output from the ADSR).
The fixed values can be altered to scale both the input and output ranges.

Related posts:

  1. Using Ring Modulation in SynthEdit

The SV Filter module.

15/02/2025 / / 0 Comments

A state variable filter is a type of active filter in electronic circuits. It consists of one or more integrators, connected in some feedback configuration (there are a few different methods of feedback). It is essentially used when a precise Q factor is required, as other multi-order filters are unable to provide. There are various design methods used in analogue circuits (which I won’t go into here), but they all give more or less the same results.

The choices of SV filter:

Note: State variable filters are all-pole filters, meaning they boost
high frequencies even when the resonance value is low.

The three styles of SV Filter

SV Filter2 – This one tends to be the one that has the most problems with overloading at high resonance levels. It has two “strengths” Single pole and Two Pole. In two pole mode the Low-pass and high-pass slopes are 12 dB per octave slopes, and band-pass or band stop (notch) modes’ slopes are 6 dB per octave.
Also, the resonant response is nonlinear in the dB scale, as the graph below shows:

Odd resonance response graph

Around 10 volts, the resonance value skyrockets close to the point of
self-oscillation. To prevent this, you may want to confine the resonance
knob’s highest value to about 9 volts, or roughly 30 dB resonance.
StateVar Filter – Much better behaved at higher resonance levels with the same switching between modes as the SV Filter2
StateVar Filter (Multi) – is essentially the same as the previous filter, but with separate outputs for Low, high, band pass and notch filter characteristics. This gives us all sorts of sonic possibilities by combining different filter outputs and mixing the levels.
The four outputs will all change the signal’s phase in different ways, sometimes creating notches.
Mixing Low Pass and High Pass outputs will create a band-reject filter.
Negative voltages are perfectly acceptable on the Input2 plug of the Level Adj, so entering something like 10 for low pass and −10 volts for high pass means that the High pass level adj will invert the signal and subtract the high-pass from the low-pass output. This produces a flat response with a resonant peak at the cutoff
frequency, which is great for adding resonant peaks to a signal.
Note: State variable filters are all-pole filters, meaning they boost
high frequencies even when the resonance value is low. This affects
band-pass and high-pass outputs more than the low-pass output. And
mixing these outputs adds a touch more gain.
See the structure below for setting up a mixable SV Filter:

Multi-output SV Filter

VA State Variable filters.
These are the updated versions of the older filters listed above, and they do have an improved high frequency range, and better stability, but still need normalizing, and the Resonance limiting To 9V
VA State Var
VA State Var (Multi)

“Oberheim” style SV Filter

This filter takes the High and Low pass filter outputs and mixes them in variable amounts with the option to invert the phase at the output of the HP filter.
This structure provides a wide range of sonic possibilities ranging through High pass, Low Pass, Bandpass, Notch, and resonance effects. The best way to find out what it’s capable of is to connect up a white noise source at the input, and have a listen (it’s also interesting to connect up the Frequency Analyser too)
I found the best results were with the mix slider set with a range of 0 to 15V and a fixed value of 15V on the Level Adj in the Low Pass signal line.

Oberheim type SV filter

Taming the SV filter.

The SV filter is versatile, but at higher resonance levels, the gain can increase to the point of clipping, this is not good, because whilst it may sound fairly good when an analogue SV filter overloads, the Synthedit module will produce some really harsh distortion. Fortunately there is a way to tame this versatile filter, with Level Adj modules, and the Waveshaper. By taking the Resonance control voltage, by the way it’s always good to limit the rage of the resonance- I have done it here using an ED Clip (Audio) module to limit the resonance to 9V, rather than the maximum allowed of 10V. Too much resonance and the filter will self-oscillate and overload.
By taking our resonance control voltage and feeding it through a waveshaper using a formula of 10-(x+5)x0.55 we can control the input and output gain in the Level Adj modules to get a fair approximation of constant signal levels at resonance settings between 0 and 9. This can be applied to all versions of the SV filter.

Normalizing the SV filter's output level.

Note: Although the StateVar filters are better ‘behaved’ than the SV filter at higher resonance levels, adding this normalization to the filters is still worthwhile.

Credit:
The Normalization structure is an adapted & updated version of the original from the book: Visual VST/i-Programming by H. G. Fortune (Editor), Peter Schoffhauzer, and David Haupt.

Related posts:

  1. VCF with multiple outputs
  2. The TD range of Synthesizer filters.
  3. Some other Useful filters in the TD range of Modules.
  4. Adding “Korg” saturation to an SV Filter.

Filters and Phase Shift.

12/02/2025 / / 0 Comments

All filters in Synthedit will by their nature exhibit some phase shift at some point in their frequency spectrum. Some filters exhibit more phase shift than others.
(Even analogue filters will introduce phase shift)

Phase shift and Analogue filters.


A basic analogue resistor–capacitor (RC) low-pass filter, as an example, will shift the output sine wave by up to 90° compared to the input sine wave. The “up to” is important—the actual phase shift generated in the circuit also depends on the frequency of the signal passing through the filter. As you can see this quickly becomes a complex subject.

Moog filters and phase shift.

A Moog ladder filter, introduces a significant phase shift as the signal frequency approaches the filter cutoff frequency, with each stage of the filter adding about 45 degrees of phase shift, which gives us a total phase shift of nearly 180 degrees at the cutoff frequency for a typical 4-stage Moog filter; it is this phase shift that contributes to the unique “warm” and resonant sound of Moog synthesizers when filtering sounds at, or near to the cutoff frequency.

SV Filters and phase shift.

An SV filter, which stands for “State Variable Filter,” introduces phase shift by design, meaning it alters the timing of different frequency components within a signal as it filters them, with the amount of phase shift varying depending on the frequency and filter settings; (this is a common to most filters, not just SV filters), but the design of an SV filter can make this phase shift far more pronounced at certain frequencies.
Key points about SV filters and phase shift:
The phase shift in an SV filter arises from the internal circuitry and the way it interacts with different frequencies, causing different time delays for various components of the signal.
The Impact on the filtered sound:
When filtering audio with an SV filter, a very noticeable phase shift can manifest as subtle changes in the sound quality, particularly affecting the timing of transients or the overall “naturalness” of the filtered sound.

“Korg MS20” filters, otherwise known as Sallen-Key filters.

The Sallen-Key filter, is a second-order active filter, with a phase shift that approaches -90 degrees at its cut-off frequency, with its phase response smoothly transitioning from 0 degrees at lower frequencies to -180 degrees at very high frequencies.
Its key characteristics include:
1) High input impedance,
2) Low output impedance,
3) Good stability, with the ability to readily adjust its cut-off frequency and quality factor (Q) by adjusting the values of its resistors and capacitors, allowing for a flexible filter design.
The Sallen-Key design used in the Korg MS20 also had the ability to go into saturation giving some unique “screaming” sounds.

Summary.
As you can see phase shift in filters is normal, and is inherent in their design and the resulting unique “flavour” imparted to the output filtered sounds. Without their built in phase response there would be no “Moog filter” sound.

Digital filters.

Most filters exhibit a phase shift of some sort, with DSP the shift is always in the form of a small delay in the signal due to the large number of complex calculations. The more efficient the computation method used, the lower the degree of phase shift introduced by the filter, unless phase shift is called for to recreate (for example) the sound of a Moog ladder filter.

For a simple 1-pole hp filter, the phase response at the cut-off frequency will be about 45 deg. As a general rule the lower the number of poles in the filter, the less the phase shift will be. All of the filters in Synthedit will introduce some degree of phase shift, this is largely unavoidable.
The degree of phase shift is dependent on the type of filter, number of poles or steepness of cutoff slope.

You can see below the phase shift that even a simple 1 pole HP filter introduces:
At 50 Hz, the two ‘scope traces are superimposed- we have an almost zero phase shift between input and output.

However at 500 Hz you can see there is a marked shift in phase (Ignoring the difference in amplitude) between the input and output signals.

Cumulative phase shift.

If you cascade (or stack) filters the phase shift is also cumulative (adds up), so if one filter gave you 45 degrees at 1kHz, two filters will give you 90 degrees phase shift at 1 kHz.

Why and when is phase shift important?

Often you wouldn’t notice that a filter was introducing phase shift, however it soon becomes apparent when you mix the filtered signal with the original “dry” signal. As the filter frequency changes you would likely notice a “phasing” effect on the sound in addition to any timbral changes from the filter itself.
You can see this in the sequence of screenshots below:

100% Low pass Moog filter.

With a mix of 50% Low pass and 50% dry signal, you can see there is a pronounced notch at 2kHz.

And with 100% dry signal we get a more or less flat white noise spectrum.

Introducing feedback (resonance) into the filter introduces further phase shifting effects as raising and lowering the resonance level will alter the phase shift quite markedly at mid range filter frequencies.

0 Resonance at a middle range frequency gives this pronounced phase shift.

Whereas with a resonance of 8.3 the signals are approaching being in phase again.

As you can see phase shift in filters is not a simple and easily predictable subject.

The only filters that I have tested in Synthedit to give a constant phase shift over their frequency range are the high and low pass SINC filters.

Related posts:

  1. SynthEdit Filters
  2. Some other Useful filters in the TD range of Modules.
  3. VCF with multiple outputs
  4. Filters: FAQ’s and tips.

Amplitude modulation.

09/02/2025 / / 0 Comments

What is Amplitude Modulation?

It’s all in the name really. We take two signals the first is our carrier, the second is the modulation. If you remember the days of medium, and long wave radio that was Amplitude Modulation applied to RF instead of AF signals. The diagram below shows a block diagram of AM in operation in a radio transmitter.


This makes quite a versatile effect in a synthesizer or FX pedal, some might say similar to Ring Modulation. But personally I class it as entirely different effect. The major difference is where a Ring Modulator (A true balanced one that is) should suppress the carrier signal, amplitude modulation does not suppress the carrier. I’m not going to get too technical (or go into the maths too deeply), but if you want to there’s a good article on Wikipedia on the subject.

Here we have 0% modulation depth:

Then 50 % modulation depth:

Next 100% Modulation depth:

You can see here how we always have an output from the modulator, and that as we apply modulation to the carrier signal we get two other signals, these are sidebands, and are created by the sum of the carrier and the modulation frequency, and the difference of the carrier and modulation frequencies.
Example: (Sorry a little bit of basic math here).
If the carrier (fc) is 440 Hz and the modulator (fm) is 200 Hz then we get a lower sideband of fc-fm=240 Hz and an upper sideband of fc+fm=640Hz. So our output will now contain 240 Hz, 440 Hz and 640 Hz. What about the 200 Hz modulation signal? This never appears as a direct signal at the output. That’s correct it only appears in the form of the sidebands.

440Hz modulated by 200 Hz:

440Hz modulated by 330Hz.

440Hz modulated by 880Hz.

Where has the lower sideband gone? Well 440Hz-880Hz= -440Hz, negative frequencies are an impossibility so it disappears. This is why we need an HP filter in the output to prevent DC and LF rumbles distorting the output.

Howe can we do this in SynthEdit?

It’s fairly easy using VCA modules if we keep one or two details in mind.
1) The VCA Response curve must be set to Linear mode for the proper modulation effect, anything else will not give the correct modulation.
2) With some combinations of carrier and modulation frequencies we can get some very loud rumbling sounds due to the difference between carrier and modulation frequencies. A high pass filter set to about 50 Hz, after the modulator will cut these out.
3) Unless the modulator structure has a bias voltage on the Modulator VCA you won’t get the true AM effect, there will only be an output when modulation is applied. This is not correct, we need to apply a 5V bias to the modulator’s Volume plug for true AM operation.
Note: Don’t be tempted to go beyond 100% modulation unless you want some horrible distortion, and aliasing by products.
Note: The Output VCA is there so that the oscillators will behave properly. If you put this in a synthesizer it’s not really needed.
Note: any Module names with an addition inside curly brackets {added} is just a comment to clarify what the module does…please don’t try and find them in SE or 3rd party modules!

The modulator structure.

The “guts” of the modulator.

Tremolo Effect.

Because the carrier signal is always present at the output we can use this effect as Tremolo as well as an effect to add extra harmonics to a signal. All we need to do is reduce the modulation frequency down to a range of say 0.1 to 5 Hz.

Are there sidebands when used as Tremolo?

Do we get any additional frequencies in the output when used with say 0.5Hz modulation as a Tremolo? No we don’t, just the original 440Hz carrier pulsing up and down in time with the modulation. Any sidebands are so close to the original carrier frequency as to be completely indistinguishable – see below.

Related posts:

  1. The SynthEdit VCA Module

Resizable slider control.

08/02/2025 / / 0 Comments

The stock Slider Control in Synthedit has one major disadvantage- It’s not resizable. This project uses third party modules, and can be re-sized by editing its panel view. Note: Resizing the actual slider knob does mean creating a new .png file for it. This control also has the option to “spring” back to a default value, which can be useful, you could use it as a pitch bend slider control for example.

The Joystick/Slider module.

The ED Joystick Image control is used for the slider control itself, there are few properties settings to note, see below:

Setting Constrain X Max to 0 stops any horizontal movement of the control by locking it to the 0 position. Leave the Constrain Y settings as Min=0 and Max=1 as we want the full range.
Ctrl Scaling factor sets how fine the control movement is when holding the Ctrl key down and moving the slider. Both the backgrounds are set as 00 for the Alpha (transparency) level so the rest of the ARGB setting can be left blank.
The Mouse Down plugs are connected so that the control will be returned to it’s default position when this option is selected.

The control background and scale grid.

The background for the control is supplied by another third party control, the DAM Rectangle, which allows us a resizable background, outline and grid with control over the colours of the background and grid, the settings are shown below.
Although I have left the background colour as preset, you could easily link the Top ARGB and Bottom ARGB to allow these as user settings.

The “Spring”.

This is the section that allows us to have a position that the control automatically returns to our user determined default position as soon as the left mouse button is released. Although we have two Spring modules connected only one needs a Reset and normalized value set ( the Y position) Note: Although it seems like only one Spring module is needed this will not work without both connected as shown.
The reset value is the position we want the control to return to, and it is the normal GUI float range of 0 to 1, so to return to the mid position a value of 0.5 must be set for the “Spring Position”. This is independent of any values given to the Min Max values for the control, and will always follow this 0 to 1 scale.

The label and value display.

Another third party module is in use here, the DAM Text Enter module as this gives us greater control over the text formatting than the stock SE text modules.
Float to text is used to for the value readout with an ED GUI Multiply (Float) so re can re-scale the readout ( for example you want to convert a range of 0 to 10 to a range of 0 to 100%- this only affects the display, not the Volts/Float outputs.

Output.

I have Included a GUI Float output, a DSP Float output, and a Volts output. The Float to Volts conversion is set to smooth (30mS).

Resizing the control.

All that need to be done is open the Panel View then drag the relevant controls to their required sizes, then lock and close the panel view.
The panel view and control settings are shown below.

Related posts:

  1. Notes about Sub Controls
  2. Creating a customizable button.
  3. SVG Slider Control.
  4. Sasha’s SVG Controls.
Newer posts »

© 2025 Synthedit help and tutorials

Theme by Anders Norén — Up ↑